Boru veya hava kanallarındaki akışkanın geçtiği güzergah boyunca enerjisini lüzumsuz yere ortama vermesini engellemek için izolasyon yapılması gerekmektedir. Ülkemizde 2008 yılında çıkarılan BİNALARDA ENERJİ PERFORMANSI YÖNETMELİĞİ ile mekanik tesisat yalıtımı için bir kural getirilmiştir. 2008 yılında yönetmelik ilk çıktığında, özellikle boru izolasyonu için asgari yalıtım kalınlıklarını veren bir tabloyu da içeriyordu. Fakat 2010 yılında bu tablo kaldırılmış ve izolasyon kalınlığının tespiti için için hesaplama yapılmasını şart koşmuştur.
Yönetmelik “Mekanik Tesisat Yalıtımı Madde 11″de şu ifade yer almaktadır:
Binaların ısıtma, soğutma, havalandırma ve klima gibi enerji kullanımını etkileyen tesisatlarında kullanılan borular, kollektörler ve bağlantı malzemeleri, vanalar, havalandırma ve iklimlendirme kanalları, sıhhi sıcak su üreticileri ve depolama üniteleri, yakıt depoları ve diğer mekanik tesisat ekipmanları, ısı köprüsüne yol açmayacak şekilde ve yüzey sıcaklığı ile iç ortam sıcaklığı arasında 5C’den fazla fark ve yüzeyde yoğuşma olmayacak şekilde yalıtılır.
Yani, yoğuşmayı bir kenara bırakırsak, izolasyon yüzey sıcaklığı ile ortam sıcaklığı arasındaki fark en fazla 5ºC olabilir. Bu kritere göre bir hesap yapılır ve bir kalınlık değeri bulunur. Şayet bu kalınlık değeri sonunda izolasyonlu yüzeyin sıcaklığı ortamın çiğ noktasının altındaysa yoğuşma oluşacak demektir. Bu durumda 5ºC kriterini daha aşağıya çekip yoğuşmanın olmayacağı yeni bir kalınlık değeri bulmak gerekir.
İzolasyon kalınlığının hesaplanması için TS EN ISO 12241:2008 “Bina donanımları ve endüstriyel tesisatlar için ısıl yalıtımı – Hesaplama kuralları” isimli standart kullanılır.

1. Isı Transferi
Isı transferi 3 farklı şekilde gerçekleşir:
İletim (Kondüksiyon): Bu transfer şekli, en bilinen yöntemdir. Temas halindeki iki maddeden yüksek sıcaklıkta olandan düşük sıcaklıkta olana doğru bir ısı geçişi olur. Tıpkı sıcak bir şeye dokununca elimizin yanması gibi.
Taşıma (Konveksiyon): Bu transfer şeklinde bir akışkan bulunması gerekir. Aslında ısıtma/soğutma tesisatlarında yapılan şey budur. Bir bölgede ısıtılan su yada hava gibi bir akışkan başka bir bölgeye gönderilerek transfer gerçekleştirilir.
Işınım (Radyasyon): Bu transfer şeklinde ısı, herhangi bir fiziksel ortama gerek duymadan elektromanyetik dalga şeklinde yayılır. Soğuk bir günde bile güneş ışınlarının bizleri ısıtması gibi.
1.1. İzolasyon kalınlığı hesaplamasında hangi ısı transfer şekli bulunur?
İzolasyon kalınlığı hesaplamasında tüm ısı transfer şekilleri mevcuttur. Bu sebeple hesaplamaların yapılması oldukça karmaşık ve zahmetlidir. Elle hesaplama yapılması çok ciddi zaman almaktadır. Bu sebeple ISO 12241’e göre hazırlanmış yazılımları kullanmak hem hata olasılığını azaltır hem de zaman kazandırır.
Şimdi, bir mahalde içinden 80ºC sıcak suyun geçtiği bir boru düşünelim. Bu borunun üzerinde yeteri kalınlıkta bir izolasyon olduğunu ve izolasyonun üzerinin de alüminyum sac ile kaplandığını varsayalım. Borunun içindeki akışkan ile boru iç çeperi arasında tşınım (konveksiyon) ile ısı transferi gerçekleşir. Boru ile izolasyon birbirlerine temas ediyor olduklarından bu ikisi arasında iletim(kondüksiyon) ile bir ısı geçişi olur. Benzer şekilde izolasyon ile sac kaplama da birbirlerine temas ettiklerinden bir iletim söz konusudur. Sac kaplama ile borunun geçtiği ortamın havası arasında yine taşınım(konveksiyon) ile ısı transferi vardır. Ayrıca alüminyum kaplamanın ışınım ile ısı transferi yapması da söz konusudur. Görüldüğü gibi 3 ısı transfer şekli de izolasyon kalınlığı hesaplamasında dikkate alınmak durumundadır.
1.2. Isı İletim Direnci
Daha önce söylediğimiz gibi tesisatımızdaki boru yada akışkanın enerjisinin ortama lüzumsuz yere yayılmasını istemeyiz. Bunun engellemek için tesisatımızla ortam arasına bir engel koymamız gerekir. Bu engel ısının geçişine karşı direnç gösterecek ve mümkün mertebe ısı transferini engelleyecektir. İzolasyon ile yapılan şey de tam olarak budur. İzolasyon malzemelerinin ısı iletim dirençleri oldukça yüksek olduğundan bu noktada işimizi görecektir.
Her malzemenin kendine has bir ısıl iletkenlik (λ) değeri vardır ve birimi W/mºK dir. Isıl iletkenlik değerinin tersine ısıl iletim direnci adı verilir. Bu malzemeler yan yana geldiklerinde tıpkı elektrik sistemlerindeki dirençlerin seri bağlanması misali ısı iletim dirençleri toplanır ve tesisatımızın ısı transferine karşı gösterdiği toplam direnç (RT) bulunur. Birimi mºK/W dır.
2. İzolasyon Kalınlığının Hesaplanması
İzolasyon kalınlığının hesaplanmasında temel formül metre başına kaybolan ısı miktarını veren aşağıdaki denklemdir.
q =( Θiç – Θdış )/ RT W/m
Burada,
Θiç ºK cinsinden akışkanın sıcaklığı
Θdış ºK cinsinden yüzey sıcaklığı
RT mºK/W cinsinden sistemin toplan ısı iletim direnci
q m başına kaybolan toplan ısı miktarı (W/m)
Bu formül yardımıyla izoleli yüzeyin sıcaklığı bulunur ve yönetmelik gereği ortam ile arasındaki farkın azami 5ºC olup olmadığı kontrol edilir. Bu denkleme bakınca hesaplamalar basitmiş gibi görünse de RT değerinin bulunması oldukça zahmetlidir.
2.1. Havada (Topraküstü) Bulunan Sistemlerde İzolasyon Kalınlığının Hesaplanması
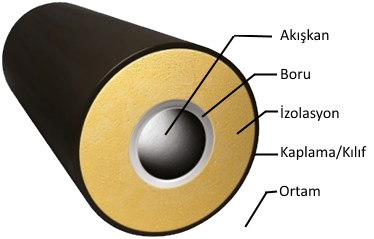

Yukarıdaki boru örneğimizde yaptığımız gibi borunun içinden dışına doğru yani akışkandan ortama doğru ilerleyerek tek tek her katmanın ısı iletim dirençlerini bulalım ve bu dirençleri toplayarak toplam ısıl iletim direncini tespit edelim.
RT = Ra + Rb + Ri + Rk + Ry

2.1.1. Akışkan (Ra )
Akışkan, boru içinde su, buhar yada başka bir sıvı/gaz olabilir. Ya da bir kanal içinden geçmekte olan hava olabilir. Bu akışkan ile boru/kanal iç yüzeyi arasında bir ısı alışverişi olacaktır. Bu ısı alışverişi taşınım (konveksiyon) türünden bir ısı geçişidir. Taşınımla geçişi yapılan ısı miktarı :
q =hiy (Θa – Θiy)
Bu formülde kullanılan hiy akışkan ile iç yüzey arasındaki ısı taşınım katsayısıdır. Birimi W/m2 ºK dir. Θa akışkan sıcaklığı, Θiy boru/kanal iç yüzeyinin sıcaklığıdır.
Bu noktada hiy değerini tespit etmek bir dizi işlem yapmayı gerektirir. İlk olarak Nusselt sayısını(Nu) bulmak gerekir. Nusselt sayısı, taşınım ısı transfer katsayısının iletim ısı transfer katsayısına oranları arasındaki ilişkiyi ifade eden bir boyutsuz sayıdır.

D, burada karakteristik uzunluktur. Borularda çap, kanallarda eşdeğer çap alınabilir. birimi m’dir. λa ise akışkanın ısıl iletim katsayısıdır, birimi W/mºK dir.
Bu formülden hiy değerini çekersek
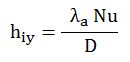
olur. λakışkan ve çap değeri D bilindiğine göre ısı taşınım katsayısını tespit etmek için Nu Nusselt sayısının bilinmesi gereklidir. Nu sayısının tespiti için ampirik formüller verilmiştir. Ancak bu ampirik formüller akışkanın akışının laminer yada türbülanslı oluşuna göre farklılık göstermektedir. Bilindiği gibi akışkanın akış türü için Reynolds Sayısı Re değerine bakılır.
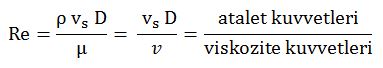
ρ : Akışkanın yoğunluğu [kg/m3 ]
vs : Akışkanın hızı [m/s]
D : Karakteristik uzunluk [m] (Çap, eşdeğer çap)
µ : Akışkanın dinamik viskozitesi [kg/ms]
v : Akışkanın kinematik viskozitesi [m2/s]
Re < 2300 ise akışkan laminer akıştadır,
10.000 > Re>2300 ise akışkan geçiş evresindedir
Re > 10.000 ise akışkan türbülanslı akıştadır.
Eğer akış laminer veya geçiş evresindeyse Nu sayısının tespiti için aşağıdaki formül kullanılır.
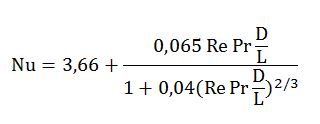
Eğer akış türbülanslı ise Nu sayısı için aşağıdaki formül kullanılmalıdır.
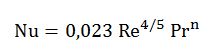
Nu sayısını veren formüllerde geçen büyüklükler şunlardır:
D : Karakteristik uzunluk [m] (Çap, eşdeğer çap)
L : Hattın uzunluğu [m]
Re : Reynolds sayısı
Pr : Prandatl sayısı
n : Isıtıcı akışkan yada soğutucu akışkan olmasına göre üs sayısı (ısıtma için n=0,4, soğutma için n=0,3)
Reynolds sayısını zaten akış türünü belirlerken hesap etmiştik. Şimdi ise Prandatl sayısı Pr’yi bulmamız gerekmektedir.
Prandatl sayısı, Pr, momentum ve ısıl dağılımların oranı olarak tanımlanır ve aşağıdaki formül ile bulunur.
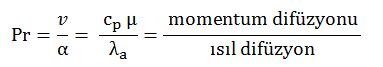
cp : Akışkanın özgül ısısı [kJ/kgºK]
µ : Akışkanın dinamik viskozitesi [kg/ms]
λa : Akışkanın ısıl iletkenlik katsayısı [W/mºK]
Bu arada şunu hatırlatmakta fayda var, akışkanın yoğunluk, viskozite, ısıl iletkenlik, özgül ısı gibi değerleri için akışkanın bulunduğu sıcaklıktaki değerlerini esas almak gerekir.
Sırasıyla, Pr sayısını ve Re sayısını bulduktan sonra Nu sayısını bulabilir ve aşağıdaki formülde zaten bilmekte olduğumuz D, çap bilgisi ve λa , akışkanın ısıl iletim katsayısını da kullanarak hiy değerini tespit edebiliriz.
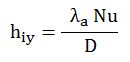
hiy akışkan ile iç yüzey arasındaki ısı taşınım katsayısıdır ve
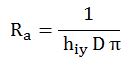
bağıntısı ile boru/kanal içindeki Ra taşınım direncini bulmuş oluruz. Çap D, borularda [m] olarak boru iç çapı Dbi , kanallarda ise [m] olarak Dki_e , eşedeğer kanal iç çapı alınır.
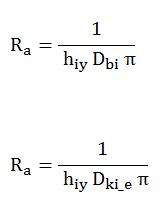

2.1.2. Boru/Kanal (Rb )
Akışkanın içinden geçtiği boru/kanal malzemesinin iç yüzeyi ile dış yüzeyi arasında bir ısı iletimi söz konusudur. Malzemenin türü ne olursa olsun ısı geçişine karşı bir miktar direnç gösteriyor olacağından iç yüzey sıcaklığı ilke dış yüzey sıcaklığı arasında bir fark olacaktır. Çelik malzemelerde ısıl iletim direnci düşük olduğundan bu ısı farkı ihmal edilebilir ama özellikle plastik türevi(HDPE, PPRC,PVC, vs.) malzemelerde ısıl iletim direnci yüksektir ve hesaba katılması gereklidir.
Silindirik şekillerde (yani borularda, yuvarlak kanallarda) ısıl iletim direnci Rb için aşağıdaki bağıntı kullanılır.
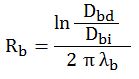
Dbd : Boru dış çapı [m]
Ddi : Boru iç çapı [m]
λb : Boru malzemesi iletkenlik katsayısı [W/mºK]
Prizmatik şekillerde (yani prizmatik kanallarda) ısıl iletim direnci Rb için aşağıdaki bağıntı kullanılır.
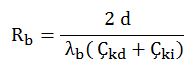
d : Et kalınlığı [m]
Çkd : Kanalın dış çevresi [m]
Çki : Kanalın iç çevresi [m]
λb : Kanal malzemesi iletkenlik katsayısı [W/mºK]
Böylece boru/kanal malzemesinin ısıl iletkenlik direnci Rb yi de tespit etmiş oluruz.
2.1.3. İzolasyon (Ri )
Boru yada kanalın etrafına uygulanmış olan izolasyonun bir kalınlığı olacaktır. Aslında tüm bu hesaplamaları yapmamızın sebebi izolasyon kalınlığını tespit etmek olduğuna göre şu aşamada izolasyon kalınlığını biliyor olamayız. Ancak şimdilik konunun anlaşılması için bildiğimizi kabul edip yolumuza devam edelim.
İzolasyon katmanının ısıl iletkenlik direncinin hesaplanması tıpkı boru/kanal malzemesinin ısıl iletkenlik direncinin hesaplanmasına benzer. Sadece boru/kanal malzemesi yerine izolasyon malzemesine ait değerleri koymak gerekir.
Silindirik şekillerde (yani borularda, yuvarlak kanallarda) izolasyon katmanının ısıl iletim direnci Ri için aşağıdaki bağıntı kullanılır.
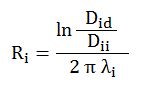
Did : İzolasyonlu dış çap [m]
Dii : İzolasyon katmanının iç çapı [m] (Aynı zamanda boru dış çapı, Dbd )
λi : İzolasyon malzemesi iletkenlik katsayısı [W/mºK]
Prizmatik şekillerde (yani prizmatik kanallarda) izolasyon katmanının ısıl iletim direnci Rb için aşağıdaki bağıntı kullanılır.
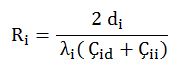
di : İzolasyon kalınlığı [m]
Çid : İzolasyon katmanının dış çevresi [m]
Çii : İzolasyonun iç çevresi [m] (Aynı zamanda kanalın dış çevresi, Çkd )
λi : İzolasyon malzemesi iletkenlik katsayısı [W/mºK]
Böylece izolasyon malzemesinin ısıl iletkenlik direnci Ri yi de tespit etmiş oluruz.
2.1.4. Kaplama/Kılıf (Rk )
Genelde uygulamalarda izolasyon katmanının üstünün koruyucu bir malzeme ile kaplandığına rastlarız. Bu kaplama alüminyum, galvaniz türü bir sac kaplama olabileceği gibi üreticisinden izolasyonun üzerinde gelen alüminyum folyo da olabilir. Ayrıca özellikle ön izolasyonlu borularda rastladığımız HDPE türü bir kılıf da kullanılıyor olabilir.
Sac ya da folyonun ısıl iletim anlamında kayda değer bir direnç göstermeyeceğini kolaylıkla tahmin edebiliriz. Fakat kılıf olarak kullanılan kaplamalar önemli ısıl direnç göstereceklerinden hesaba alınmalıdır.
Silindirik şekillerde (yani borularda, yuvarlak kanallarda) kaplama/kılıf katmanının ısıl iletim direnci Rk için aşağıdaki bağıntı kullanılır.
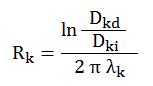
Dkd : Kaplama/Kılıf dış çapı [m]
Dki : Kaplama/Kılıf iç çapı [m] (Aynı zamanda izolasyonlu çap, Did )
λk : Kaplama/Kılıf malzemesi iletkenlik katsayısı [W/mºK]
Prizmatik şekillerde (yani prizmatik kanallarda) kaplama/kılıf katmanının ısıl iletim direnci Rk için aşağıdaki bağıntı kullanılır.
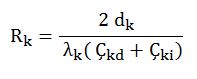
dk : Kaplama/Kılıf kalınlığı [m]
Çkd : Kaplama/Kılıf katmanının dış çevresi [m]
Çki : Kaplama/Kılıf katmanının iç çevresi [m] (Aynı zamanda izolasyon katmanının dış çevresi, Çid )
λk : Kaplama/Kılıf malzemesi iletkenlik katsayısı [W/mºK]
Böylece Kaplama/Kılıf malzemesinin ısıl iletkenlik direnci Rk yı da tespit etmiş oluruz.

2.1.5. Dış Yüzey Direnci (Ry)
Tıpkı en başta akışkan ile boru/kanal çeperi arasında olan ısı alışverişi gibi yalıtım uyguladığımız boru/kanal bulunduğu ortamla bir ısı alışverişi yapacaktır. Bu ısı alışverişi iki şekilde olur. İlki ışınımla(Radyasyon) olan kısımdır ve kaplama/kılıf malzemesiyle yakından ilgilidir. İkinci kısım ile taşınımla olan ısı transferidir.Bu kısım ise boru /kanal sisteminin yatay/dikey olmasına, açık/kapalı ortamda olmasına, rüzgarın varlığı gibi bir takım büyüklüklere bağlıdır.
2.1.5.1 Yüzey Direncinin Isı Işıma(Radyasyon) Katsayısı (hr)
Yalıtım uyguladığımız boru yada kanalımız (şayet toprak altında değilse) bulunduğu ortamla ışıma ile bir ısı alışverişi yapacaktır. Özellikle kaplama malzemesinin evsafının bu ısı alışverişinde etkisi çok büyüktür.
hr dış yüzey ile ortam arasındaki ışımaya ait ısı transfer katsayısı hr değerinin tespiti şu şekilde yapılır.
![]()
ar : Sıcaklık faktörü [ºK3 ]
Cr : Işınım katsayısı [W/m2 ºK4 ]
hr : Dış yüzey ile ortam arasındaki ışımaya ait ısı transfer katsayısı [W/m2 ºK ]
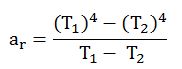
T1 : Yüzey sıcaklığı [ºK ]
T2 : Ortam sıcaklığı [ºK ]
Lütfen ar değerini hesaplarken T1 ve T2 sıcaklıklarının [ºK ] olduğuna dikkat ediniz.[ºC ] kabul ederseniz yanlış sonuç bulursunuz. Isı transferi hesaplarında [ºK ] yerine [ºC ] kullanmak çoğu zaman sonucu etkilemez ama ar için bu durum farklıdır.
![]()
ε : En dış katmanın (kaplama, kılıf yada izolasyonun kendisi) yayınım katsayısı[- ]
σ : 5,67×10-8 [W/m2 ºK4]
Görüldüğü gibi, ε yani en dış katmanın yayınım katsayısının bilinmesine ihtiyacımız vardır. Bu değer için ISO 12241’de şu tablo verilmiştir:
| Kaplama | ε | Cr |
| Alüminyum (Parlak) | 0,05 | 0,28×10-8 |
| Alüminyum (Kirli) | 0,13 | 0,74×10-8 |
| Galvaniz Sac (Temiz) | 0,26 | 1,47×10-8 |
| Galvaniz Sac (Kirli) | 0,44 | 2,49×10-8 |
| Paslanmaz Çelik | 0,15 | 0,85×10-8 |
| Alüminyum Çinko | 0,18 | 1,02×10-8 |
| Metal olmayan | 0,94 | 5,33×10-8 |
Bu tablo yardımıyla ε değerini de tespit dip yukarıda verilen formüllerde yerine koyunca hr değerini bulmuş oluruz.

2.1.5.2 Yüzey Direncinin Isı Taşınım (Konveksiyon) Katsayısı (hc)
Tıpkı akışkan ile boru/kanal çeperi arasındaki taşınımla yapılan ısı transferi gibi en son katmanla(kaplama, kılıf yada izolasyonun kendisi) ortamın havası arasında da taşınımla bir ısı alışverişi olur.
hc dış yüzey ile ortam arasında taşınım ısı transfer katsayısı [W/m2 ºK ] şu şekilde bulunur:
hc değerinin tespiti oldukça fazla parametreye ve şarta bağlıdır ve ISO 12241’de hesap yöntemi detaylıca verilmiştir. hc değeri sıcaklık ve çap bilgileri dışında boru/kanal sistemimizin kapalı yada açık ortamda bulunmasına, yatay yada dikey olarak yerleştirilmiş olmasına, hava akışının laminer yada türbülanslı olmasına bağlıdır. Bu şekilde 8 farklı durum oluşmaktadır. Tüm bu durumlara göre hc değerinin farklı farklı formülleri vardır. Kolaylık olması açısından kullanılacak formüller aşağıdaki tabloda gösterilmiştir:
| Lokasyon | Dikey yerleşim | Yatay yerleşim | ||
| Laminer hava akışı | Türbülanslı hava akışı | Laminer hava akışı | Türbülanslı hava akışı | |
| Kapalı Ortam (Bina içi) |
Eşitlik a | Eşitlik b | Eşitlik c | Eşitlik d |
| Açık Ortam (Bina dışı) |
Eşitlik e | Eşitlik f | Eşitlik e | Eşitlik f |
Eşitlik a ( Kapalı ortamda, dikey yerleştirilmiş, laminer hava akışlı sistem)
Eğer [Dbi3 (Θortam – Θyüzey )]≤10 m3 ºK ise akış laminerdir.
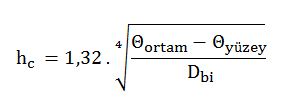
Eşitlik b ( Kapalı ortamda, dikey yerleştirilmiş, türbülanslı hava akışlı sistem)
Eğer [Dbi3 (Θortam – Θyüzey )]>10 m3 ºK ise akış türbülanslıdır
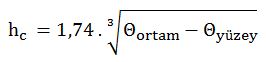
Eşitlik c ( Kapalı ortamda, yatay yerleştirilmiş, laminer hava akışlı sistem)
Eğer [Dkd3 (Θortam – Θyüzey )]≤10 m3 ºK ise akış laminerdir.
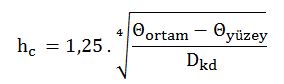
Eşitlik d ( Kapalı ortamda, yatay yerleştirilmiş, türbülanslı hava akışlı sistem)
Eğer [Dkd3 (Θortam – Θyüzey )]>10 m3 ºK ise akış türbülanslıdır
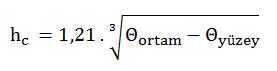
Eşitlik e ( Açık ortamda, yatay yada dikey yerleştirilmiş, laminer hava akışlı sistem)
Eğer vw . Dkd ≤ 0,00855 m2 /s ise akış laminerdir
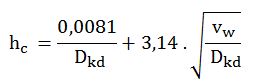
Eşitlik f ( Açık ortamda, yatay yada dikey yerleştirilmiş, türbülanslı hava akışlı sistem)
Eğer vw . Dkd > 0,00855 m2 /s ise akış türbülanslıdır.
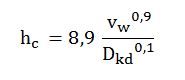
Toplam 6 eşitlikte kullanılan büyüklükler ise şunlardır:
hc : Dış yüzey ile ortam arasındaki taşınıma ait ısı transfer katsayısı [W/m2 ºK ]
Dbi : Boru/Kanal içi çapı (eşdeğer çapı) [m]
Θortam : Ortam sıcaklığı[ºK]
Θyüzey : En dış yüzey (kaplama, kılıf yada izolasyonun kendisi) sıcaklığı[ºK]
Dkd : Karakteristik uzunluk [m] (Kaplama/Kılıflı dış çap, eşdeğer çap)
vw : Rüzgar hızı [m/s]
Boru/kanal sisteminin kapalı/açık ortamda olmasına, yatay/dikey olmasına ve laminer/türbülanslı hava akışında olmasına göre yukarıdaki eşitliklerden bir tanesini kullanarak hr değerini bulmuş oluruz.
Gelinen nokta itibariyle dış yüzey ile ilgili hem hr değerini hem de hc değerini bularak toplam yüzey direncine ait hy katsayısını buluruz.
hy = hr + hc
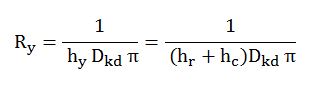
Ancak şu noktaya dikkat çekmek gerekir: Tıpkı izolasyon katmanının direncini bulurken kalınlık bilgisini bilmememize rağmen biliyormuş gibi devam ettiğimiz gibi burada da aynı varsayımı yapmak durumunda kaldık. Çünkü eşitliklerde geçen Dkd yani en dış çap değeri, izolasyon kalınlığını bilmeden tespit edilemez.
2.1.6. Toplam ısıl iletim direnci (RT)
Akışkandan ortama doğru ilerleyerek tek tek her katmanın ısı iletim dirençlerini bulduğumuza göre artık izolasyonun toplam ısıl iletim direncini de tespit etmiş oluyoruz.
RT = Ra + Rb + Ri + Rk + Ry [mºK/W]
Artık akışkandan ortama doğru her bir katmanın sıcaklık değerlerini bulmak mümkündür. Sırasıyla katmanlarımıza ait sıcaklık ve dirençler şöyledir:
| Θa akışkan sıcaklığı | |
| Ra akışkan ile içyüzey arasındaki taşınım direnci | |
| Θiy boru/kanal iç yüzey sıcaklığı | |
| Rb boru/kanal malzemesi ısı iletim direnci | |
| Θb boru/kanal dış yüzey sıcaklığı, izolasyon katmanı iç yüzey sıcaklığı |
|
| Ri izolasyon malzemesi ısı iletim direnci | |
| Θi izolasyon katmanı dış yüzey sıcaklığı, kaplama/kılıf katmanı iç yüzey sıcaklığı |
|
| Rk kaplama/kılıf malzemesi ısı iletim direnci | |
| Θk =Θyüzey kaplama/kılıf katmanı dış yüzey sıcaklığı | |
| Ry yüzey(ışınım ve taşınım) direnci | |
| Θortam ortam sıcaklığı |
Her bir katmanın sıcaklık değerleri için şu bağıntılar kullanılır:

Geldiğimiz aşamada artık biraz matematik yapmamız gerekmektedir. Son sırada bulunan denklemden yola çıkarsak gerekli izolasyon kalınlığını tespit edebiliriz.
(Θyüzey – Θortam) değerinin yönetmelik gereği 5ºC olması gerektiği yazının başında ifade edilmişti.Buradan yola çıkarak çözülmesi gereken denklemi oluşturalım:
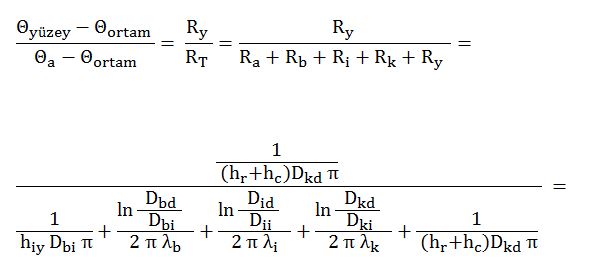

Görüldüğü gibi çözümü oldukça zor bir denklem oluşmuştur. Bunu bilgisayar yazılımı kullanarak iterasyonla çözmek gerekecektir. Çözmeye çalıştığımız di: izolasyon kalınlığı değeridir.
Ancak hc değeri de yerleşimin, ortamın, akış türünün bir fonksiyonu olarak zaman zaman dış çapa bağlıydı. Bu şartlardan yerleşimi (Yatay, dikey durumu) ve ortamı(açık, kapalı durumu) başta biliyor olduğumuzdan azami 2 adet hc değeri için çözüm yapıp şartların uyuşup uyuşmadığını kontrol etmek gerekir.
İşleri karmaşıklaştıran bir nokta daha vardır: Bilindiği gibi her malzemenin ısıl iletkenlik katsayısı λ, sıcaklıkla değişir. Bu nedenle denklemlerde kullanılan ısıl iletkenlik katsayıları için iç yüzey sıcaklığı ile dış yüzey sıcaklığının aritmetik ortalaması bulunur ve bu sıcaklık değerindeki ısıl iletkenlik katsayısı denklemlerde esas alınır. Bu durumda yukarıdaki denklemde λi yani izolasyon malzemesi ısıl iletkenlik katsayısı da izolasyon kalınlığının bir fonksiyonu olacaktır. İterasyon yapılırken bu nokta da hesaba katılabilir ama akışkan sıcaklığındaki değeri alıp emniyetli tarafta kalmak da tercih edilebilir.
Aynı denklemi prizmatik kanallar için de yazarsak:


2.1.7 Yoğuşma
Eğer izolasyonlu yüzeyin sıcaklığı ortam havasının çiğ noktası sıcaklığından düşükse izolasyonlu yüzey üzerinde yoğuşma gerçekleşecektir. Yukarıdaki denklemi hiç çözmeye başlamadan önce ortamın çiğ noktası sıcaklığı tespit edilmelidir. Eğer yönetmeliğin istediği 5ºC fark yeterli gelmiyorsa yani yoğuşma olmaması için izolasyonlu yüzeyin sıcaklığı ile ortam sıcaklığı farkının 5ºC’den de az olması gerekiyorsa temel kriter olarak bu sıcaklık farkıyla denklem çözülür.

Örneğin, 30ºC %50 nemli bir ortamda içinden 7ºC su geçen bir izolasyonlu boru düşünelim. 30ºC %50 nemli bir ortamda çiğ noktası sıcaklığı 18,3ºC dir. Eğer yapılan izolasyon sonrası yüzey sıcaklığı 18,3ºC nin altında alırsa yoğuşma olayı gerçekleşecek, kalmazsa yoğuşma olayı gerçekleşmeyecektir. Aynı ortamda bu sefer %80 nem olduğunu düşünelim. 30ºC %80 nemli bir ortamda çiğ noktası sıcaklığı 26,1ºC dir. Eğer izolasyonlu yüzey sıcaklığını 5ºC kriterine göre yapıp yüzey sıcaklığını 25ºCye getirirsek çiğ noktası sıcaklığının altında kalınacağından yoğuşma olacaktır. Bu sebeple sıcaklık farkı kriterini 3,5ºC dolaylarıa getirip izolasyon kalınlığını ona göre seçmemiz gerekir.
2.2. Toprakaltı Boruları
Boru tesisatımız toprak altındaysa izolasyon kalınlığı hesabımızda bazı farklılıklar oluşur. Herşeyden önce havayla ısı alışveriş yapmadığı için ışımadan ve konveksiyondan kaynaklanan yüzey direnci ortadan kalkar. Onun yerine varsa dolgu malzemesi direnciyle toprak direnci girer. Yani yukarıdaki bölümde yaptığımız sıralamayı tekrar yaparsak; önce akışkan, sonra boru, sonra izolasyon, sonra kılıf/kaplama malzemesi gelir. Buraya kadar herşey aynı, bu noktadan sonra toprakaltı borularda dolgu malzemesi ve toprak gelir.
Dolgu malzemesi dediğimiz şey aslında şudur: Toprakaltı boru tesisatı yapmak için bir kanal açtığımızı düşünelim. Eğer kanalı toprağın kendi evsafından daha farklı bir malzemeyle yastıklar ve boruyu sararsak bu durumda dolgu yapmış oluruz. Mesela kum ile… Neticede bu dolgu da borunun etrafına yapılmış bir izolasyon katmanı olarak görev yapacaktır.
Bu durumda toplam ısı iletim direncimiz, sırasıyla akışkan taşınım, boru malzemesi iletim, izolasyon malzemesi iletim direnci, kaplama/kılıf malzemesi iletim direnci, dolgu malzemesi iletim direnci ve toprak iletim dirençlerinin toplamıdır.
RT = Ra + Rb + Ri +Rk + Rd + Rt
Dolgu katmanına kadar, tüm direnç hesaplamaları yukarıdaki hesaplarla aynıdır. Dolgu ve toprak dirençleri için ise şu şekilde hesaplama yapılır.
2.2.1 Dolgu Malzemesi (Rd )
Dolgu malzemesi de borunun etrafındaki bir izolasyon katmanı gibi davranır. Elbette pratikte silindirik borunun etrafına silindirik bir dolgu yapılamadığından bu dolgu katmanı kesiti, kenar uzunluğu a olan bir kare olarak düşünülür. Direnç hesabı yaparken a değerinden yola çıkarak eşdeğer bir çap, Dd belirlenir ve direnç o şekilde hesaplanır.
Dd = a . 1,073
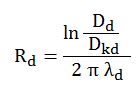
Rd : Dolgu malzemesi ısı iletim direnci [m ºK/W ]
Dd : Dolgu malzemesi katmanı eşdeğer çapı Dd = a . 1,073 [m ]
Dkd : Kılıflı/Kaplamalı boru dış çapı [m]
λd : Dolgu malzemesi iletkenlik katsayısı [W/mºK]
Eğer dolgu malzemesi kullanılmıyorsa doğal olarak Rd =0 olacaktır.
2.2.2 Toprak (Rt )
Dolgu malzemesinden sonra en dış katman olarak artık toprak vardır. Işınım ve konveksiyon olmadığından ortam olarak havada bulunan boru tesisatına nispeten toprak direncinin hesabı kolaydır.
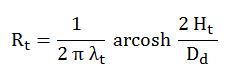
Rt : Toprak ısı iletim direnci [m ºK/W ]
Dd : Dolgu malzemesi katmanı eşdeğer çapı Dd = a . 1,073 [m ]
Ht : Toprak yüzeyi ile boru ekseni arasındaki mesafe [m]
λt : Toprak iletkenlik katsayısı [W/mºK]
2.2.3. Toprakaltı borularda toplam ısıl iletim direnci (RT)
Rd dolgu malzemesi direnci ve Rt toprak direnci yukarıda anlatıldığı gibi bulunduktan sonra RT toplam direnci bulabiliriz.
RT = Ra + Rb + Ri +Rk + Rd + Rt
Toplam direnç bulunduktan aşağıdaki bağıntılarla her bir katmanın yüzey sıcaklığı hesaplanabilir.
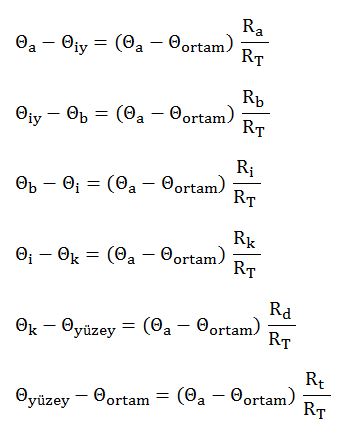
Burada dolgu katmanının boru izolasyonun bir parçası olduğunu düşünerek en dış yüzey olarak dolgu katmanının toprakla birleştiği yüzeyi esas alalım. Ortan sıcaklığı yani toprak sıcaklığı ile dolgu yüzeyi sıcaklığı arasındaki fark bizim için kriter olacaktır. Her iki sıcaklık arasındaki farkın 5ºC olacağı esas alınıp izolasyon kalınlığı hesabı yapılabilir. (Gerçi yönetmelikte 5ºC koşulu iç ortamdaki hatlar için verilmiştir. Toprakaltı için böyle bir koşul yoktur.)
3. Dikkat Çeken Çıkarımlar
İzolasyon yapmamızın temel amacı akışkanının ısı enerjisinin ortama kaçmamasıdır. Bu nedenle ortam ile akışkan arasına ısıl anlamda direnç gösterecek izolasyon malzemesi koyarız. Bu direnç ne kadar büyük olursa ısıl anlamda o kadar iyi izolasyon yaptığımız söylenebilir. Bu anlamda yukarıda verilen formüllerden yola çıkarak bazı yorumlar yapmamız mümkündür.
- İzolasyon üzeri kaplama yapılması gerekli izolasyon kalınlığını arttırır.
Kaplama malzemesinin cinsi ışınımla yapılan ısı transferi miktarı ile yakından ilgilidir. Yukarıda anlatılan hr dış yüzey ile ortam arasındaki ışımaya ait ısı transfer katsayısının formülü şöyleydi.
![]()
Burada Cr ışınım katsayısı azalırsa hr değeri de azalacaktır. hr ile ısıl direnç ters orantılı olduğundan sonuçta R değeri artacaktır. Mesela izolasyonun üzerini Cr değeri 5,33×10-8 [W/m2 ºK4 ] olan PVC bir malzeme yerine Cr değeri 0,28×10-8 [W/m2 ºK4 ] olan parlak alüminyum ile kaplarsak Cr değerimiz yaklaşık 19 kat azalmış olacaktır. Buna paralel hr değerimiz de 19 kat azalacaktır. Sonuçta Ry, yüzey direncimiz belli bir oranda artmış, haliyle RT, toplam direncimiz de artmış olacaktır.
Şimdi burada bir çelişkili durum var gibi algılanabilir. Zira toplam direncimiz artınca ihtiyaç duyduğumuz izolasyon kalınlığının az olmasını, haliyle az maliyetle karşılaşmayı bekleyebiliriz. Fakat bu noktada ufak bir ayrıntı vardır. Bu ayrıntıyı en güzel elektrik analojisiyle anlatabiliriz.
Şimdi her bir katmanımızın bir elektrik devresinde direnç olduğunu, sıcaklık farkının da gerilim farkı olduğunu düşünelim ve devremizi oluşturalım.
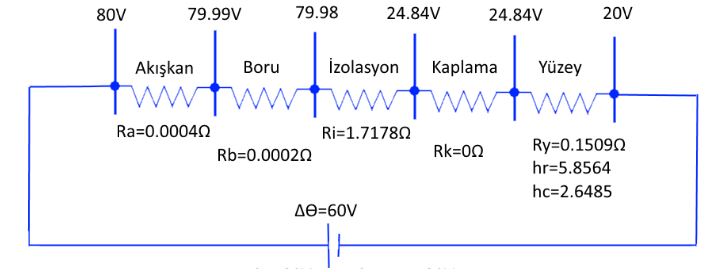
Burada örnekte, 20ºC kapalı ortamda,yatayda, içinden 80ºC akışkan geçen kayayünü (borutipi, 80kg/m3) izolasyonlu ama dış kaplaması olmayan bir boru sistemi kurguladık. Yapılan hesaplamalar neticesinde 40,79mm izolasyon kalınlığı ihtiyacı bulundu. Görüldüğü gibi yüzey direnci üzerinde yaklaşık 5ºC (Yani elektrik analojisinde (24,84-20=4,84V) olması sağlandı:
Elektrikten bilindiği gibi her direncin üzerinden aynı değerde akım dolaşır. Haliyle şu eşitliği yazmak mümkündür:
(Ɵa – Ɵy ) /( Rb + Ra + Ri +Rk) = (Ɵy – Ɵortam ) /Ry
Görüldüğü gibi Ri ve Ry doğru orantılıdır. Yani Ry arttıkça eşitliği sağlayıp dengeye gelmek için Ri de artacaktır. Eğer arttırılmazsa yüzey ile ortam arasındaki sıcaklık farkı değeri 5ºC nin üzerine çıkacaktır ve yönetmeliğin koşulu sağlanamayacaktır.
Yukarıdaki örnekteki aynı devreyi bu kez parlak alüminyum kaplama ile çözersek:
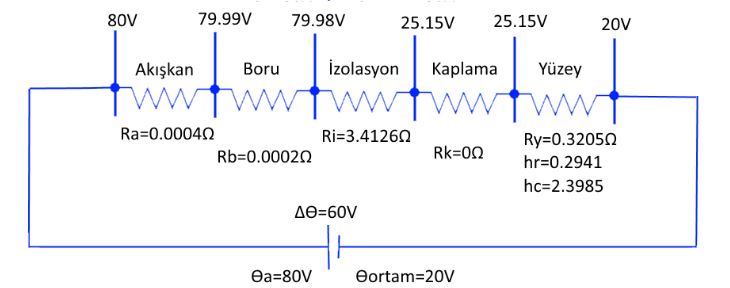
Görüldüğü gibi yüzey üzerindeki yaklaşık 5V farkını tutturabilmek için Ri de arttırılmıştır. Özetle alüminyum kaplama yapıldığından kullanılan izolasyonun kalınlığı 40.79mm den 101.6mm’e çıkmıştır. Eğer galvaniz kaplama yapılsaydı 62mm olacaktı. Yani özellikle alüminyum folyo kaplı izolasyonları kullanırken bu konuyu hatırlamakta fayda vardır.
- Rüzgarlı ortamlarda yapılması gerekli izolasyon kalınlığını azalır.
Yukarıdaki örneğin ilk kısmında kaplama yokken izolasyon kalınlığını, 40.79mm olarak bulmuştuk. Aynı tesisatı açık ortamda 2,5m/s hızlı bir rüzgarlı ortama taşırsak gerekli izolasyon kalınlığı 13.10 mm’ye düşer.
Bu durum da konveksiyonla taşıma katsayısı hc ile yakından ilgilidir.
Hatırlanacağı gibi hc rüzgar hızı ile doğru orantılıdır. Rüzgar hızı arrtıkça, hc de artacak ve Ry azalacaktır. Kaplama olayındaki durumdan hatırlanacağı gibi Ry azaldıkça izolasyon kalınlığı azalacak, Ry arttıkça izolasyon kalınlığı artacaktır. Neticede rüzgar hızı arttıkça ihtiyaç duyulan izolasyon kalınlığı azalacak, rüzgar hızı azaldıkça ihtiyaç duyulan izolasyon kalınlığı artacaktır.
- Toprakaltı borularda dolgu malzemesi izolasyon görevi görür
Toprakaltı borularda kum serilmesi ve borunun kumla kaplanmasının genelde taş, kaya parçası, keskin maddeler gibi bir takım yabancı maddelerin boruya zarar vermesi olasılığına karşı koruyucu olduğu düşünülür ki bu zaten doğrudur. Ancak bunun yanında bu durum toprakaltı borularda gerekli izolasyon kalınlığını azaltacak yani izolasyon maliyetini düşürecek bir faktör olarak da kullanılır.
- Toprakaltı borularda toprağın nem oranı arttıkça izolasyon kalınlığı azalır
Toprak ısı iletim katsayısı topraktaki nem oranı ile doğru orantılıdır. Yani nem arttıkça ısı iletim katsayısı da artar. Yani toprak ısıyı iyi iletir, yani toprağın ısıya karşı gösterdiği direnç azalır.
Direnç azalınca, tıpkı elektrik analojisinde yapıldığı gibi izolasyon direncinin yani kalınlığının da azalması gerekir.
- İzolasyon malzemesinde öncelikli yoğunluk değil kalınlıktır.
İzolasyon malzemelerinde ısıl iletim katsayıları yoğunlukla doğru orantılı olarak değişmez. Örneğin 55 kg/m3 yoğunluklu boru tipi camyünü ısıl iletkenlik değeri 0,0425 W/mºK iken aynı ürünün 100kg/m3 yoğunluklusu için ısıl iletkenlik değeri 0,0397 W/mºK dir.
20ºC kapalı ortamda,yatayda, içinden 80ºC akışkan geçen camyünü (borutipi, 55kg/m3 ) izolasyonlu ama dış kaplaması olmayan bir boru sistemi için izolasyon kalınlığı 42,49mm dir. Aynı sistemde camyünü (borutipi, 100kg/m3 ) kullanırsak gerekli izolasyon kalınlığı 40,06mm olacaktır. Görüldüğü gibi, yoğunluk değeri neredeyse 2 kat artmasına rağmen gerekli izolasyon kalınlığı sadece 2mm azalmıştır.
- Hava kanallarında kanal iç yüzey direnci önemlidir.
Borularda akışkan sıvı ise ve hatta özellikle su ise, borunun iç yüzeyi ,le akışkan arasında oluşan yüzey direnci kayda değer bir büyüklükte değildir. İhmal edilmesinde bir sakınca yoktur. Ancak buharda, gazlarda ve hava kanallarında iç yüzey direnci kaydadeğer büyüklüktedir. İhtiyaç duyulan izolasyon kalınlığını azaltan yani maliyeti düşüren yönde katkısı olur. Özellikle hava kanallarında akışkanın hava olmasından dolayı iç yüzey direnci yüksektir. Bu sebeple seçilen izolasyon kalınlığı nispeten incedir.
Mesela içinden 10m3/h, 80ºC sıvı su geçen DN50 çaplı siyah borunun iç yüzey direnci 0.0009 mºK/W dır. İçinden 5000m3/h, 30ºC %50RH nemli hava geçen 800x700mm hava kanalının 0.015 mºK/W dır.
Kaynaklar:
Binalarda Enerji Performansı Yönetmeliği
CINI (Committee Industrial Insulation)
İzocam Tesisat Yalıtım Hesaplama Programı