Herhangi bir sistemde 2 nokta arasında akış gerçekleşebilmesi için bu iki nokta arasında potansiyel farkı olması gerekir. Eğer A noktasındaki potansiyel, B noktasındaki potansiyelden yüksekse A noktasından B noktasına bir akış olacaktır. İki nokta arasındaki potansiyel farkı boru içindeki sıvının akışı sırasında boru iç cidarlarına sürtünerek kaybolan enerjiyi karşılamak için kullanılır. Boru basınç kaybı dediğimiz şey aslında budur.
Boru basınç kaybı hesaplama metotları
Boru basınç kaybı aslında oldukça karışık bir formülasyona sahiptir. Bu nedenle hesabın yapılması için farklı metotlara başvurulmaktadır. Kayıp değerinin hesaplanması için belli başlı 5 tane metot vardır.
- Darcy-Weisbach Formülü
- Colebrook-White Denklemi ve Moody Diyagramı
- Swamee-Jain Metodu
- Hazen – Williams Metodu
- Manning Metodu
Bu hesaplardan Hazen-Williams metodu, Amerika’da en çok tercih edilen, Darcy-Weisbach Avrupa’da en çok tercih edilen metotdur. [1]
Biz bu yazımızda Darcy-Weisbach Metodu üzerinde duracağız.
Darcy-Weisbach Formülü
Borulardaki sürtünme basınç kayıplarını Darcy-Weisbach formülü ile hesaplayabiliriz. Darcy-Weisbach formülü aşağıdadır..
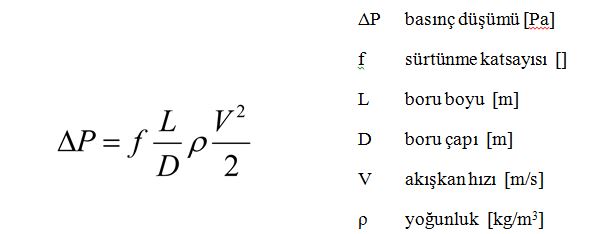
Formül aslında oldukça basit görünümdedir. Ancak buradaki tüm zorluk f, sürtünme katsayısının tespitinde yatmaktadır. Onun dışındaki tüm veriler (boru boyu, çapı, akışkan hızı, akışkan yoğunluğu) zaten bilinmektedir. f, sürtünme katsayısı 2 temel büyüklüğe bağlıdır. İlki akışın türünü ifade eden Reynolds sayısına, ikincisi ise borunun pürüzlülük katsayısına. Reynolds katsasyısı da özünde akışkanın hızına, yoğunluğuna, viskozitesine, borunun çapına bağlı olduğundan f, sürtünme katsayısı da haliyle tüm bu değişkenlere bağlı olmaktadır.
Reynolds Sayısı
Basınç kaybı hesabında daha fazla detaya girmeden önce Reynolds sayısını hatırlamak gerekir. Reynolds sayısı, boru içinde hareket eden sıvının akış türünün tespitine yardımcı olur. Akış türünün laminer (düzgün) akış olması yada türbülanslı akış olması boru basınç kaybını yakından ilgilendirir. Bu nedenle basınç kaybı hesabına başlamadan önce boru içindeki akışın türünü tespit etmemiz gerekir.
Reynolds sayısı, özetle akışı artması lehindeki kuvvetlerin akışın azalması lehindeki kuvvetler oranı olup boyutsuz bir büyüklüktür. Yani, fiziksel olarak Reynolds sayısı, bir akışkanın, atalet kuvvetlerinin (vs ρ) viskozite kuvvetlerine (μ/d) olan oranıdır.
Eğer bu denklemin sonucunda bulunan Re saysı değerlendirilir.
Re<2300 ise akış LAMİNERdir.
2300<Re<4000 ise akış laminerden türbülanslı akışa GEÇİŞ EVRESİndedir.
Re>4000 ise akış TÜRBÜLANSLIdır.
f Sürtünme Katsayısının Bulunması
f sürtünme katsayısının hesabı laminer akış için oldukça kolaydır.
Görüldüğü gibi, laminer akışta karışık matematiksel denklemlere girmeden f sürtünme katsayısı kolayca hesaplanır, Darcy-Weisbach formülünde de yerine konarak boru basınç kaybı tespit edilmiş olur.
Ancak akış, laminer değilde geçiş evresindeyse yada türbülanslı ise farklı bir formüle başvurmak gerekir. Bu tür akışlardaki f sürtünme katsayısının hesabı için 1937 yılında Colebrook-White aşağıdaki denklemi ortaya koymuştur.
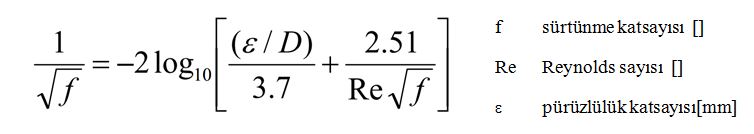
Görüleceği gibi bu denklem oldukça karışıktır ve kök bulmak için sayısal analiz yöntemlerine başvurmak gerekir. Özellikle bilgisayarların yaygın olmadığı dönemlerde bu tür denklemlerin hesaplanması son derece güç olduğundan bazı yaklaşım formülleri ortaya konmuştur. Bu formüller Colebrook-+White denkleminin kökünün bulunmasını belli bir hata payı ile sağlamaktadır. Bu yaklaşım denklemlerinin bazıları şunlardır: Goudar-Sonnad denklemi, Serghides denklemi, Romeo denklemi, Ziagrand denklemi, Chen denklemi, vs. Bu denklemler arasında en az hata ile sonuç veren denklem Goudar-Sonnad denklemidir. [2]
Bu noktada bir bir tercih yapmak söz konusu olabilir. Colebrook-White denkleminden f sürtünme katsayısını çekmek için bilgisayar yardımıyla iteratif işlemler yapılarak doğru sonuç bulunabilir. Ya da hiç sayısal analiz yöntemlerine ve iteratif işlemlere girmeden Goudar-Sonnad denklemiyle (yada tercih edilecek başka bir yaklaşım denklemiyle) belli bir hata payıyla f sürtünme katsayısı bulunabilir.
Goudar Sonnad Denklemi
Colebrook-White denkleminden f sürtünme katsayısının çekilmesi için Gounar-Sonnad tarafından ortaya konan yaklaşım denklemi aşağıdadır. Bu denklem(ler)de Re , pürüzlülük katsayısı ve boru çap değeri yerlerine konarak f sürtünme katsayısı iteratif işlemler girmeden tespit edilebilir.
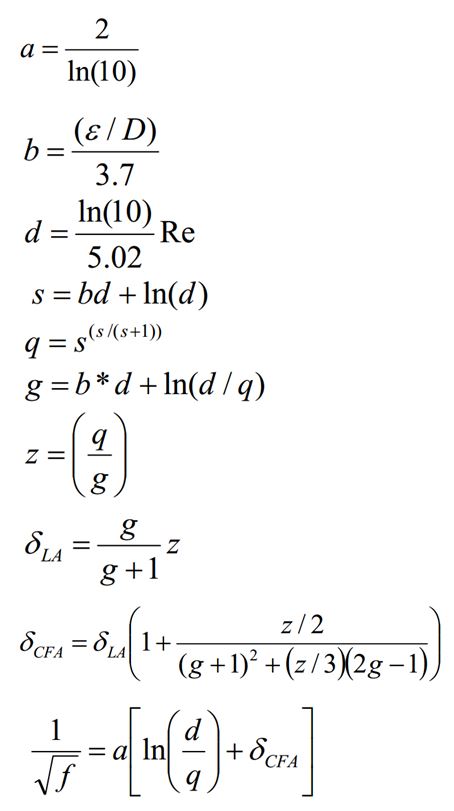
Boru Basınç Kaybının Hesaplanması Programı
Yukarıda anlatılanların excel ile formülasyonun kurulduğu programı aşağıdaki bu bağlantıdan indirebilirsiniz.
Kaynaklar:
[1]Pompa ve hidrofor sistemlerinde kullanılan sürtünme kaybı hesap metotları
[2]Sürtünme denklemleri ve hata analizi
